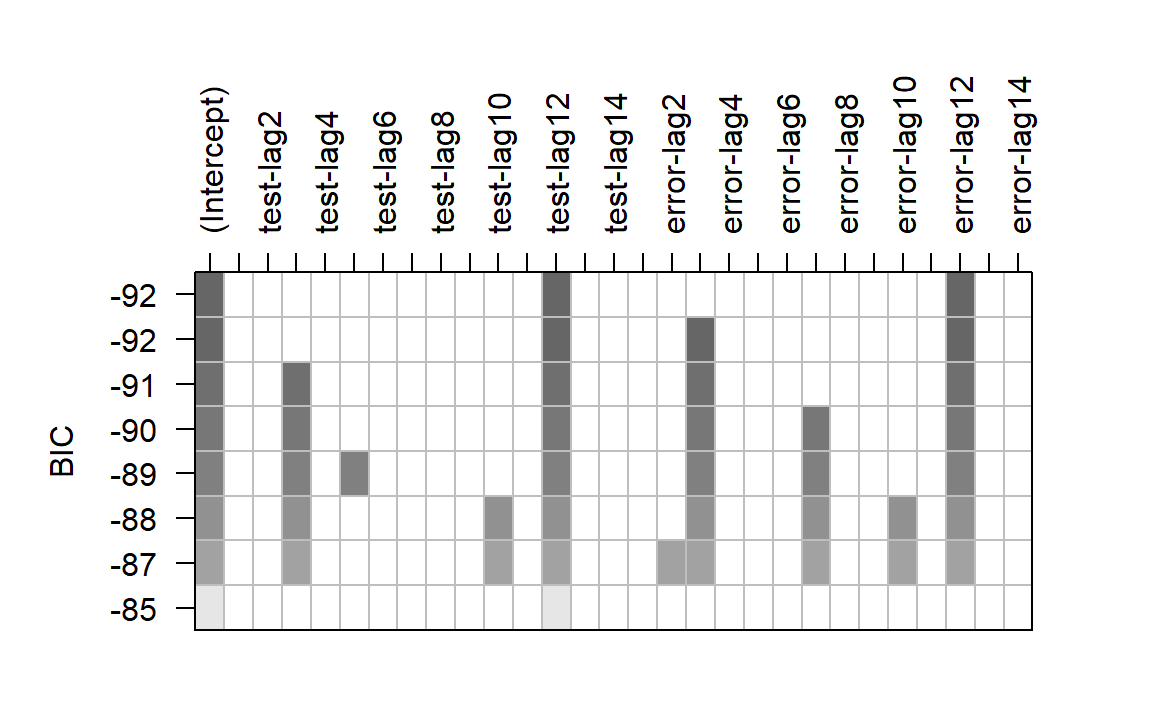
3 模型识别

本章主要学习，对于给定的时间序列，如何选取适当的\(p,d,q\)，从而建立\(ARIMA(p,d,q)\)模型。

library(TSA)
library(uroot)
set.seed(1014)

3.1 主要方法

利用样本自相关函数估计\(MA(q)\)模型的自相关函数，再利用模型自相关函数的截尾性估计\(q\)
利用样本偏自相关函数估计\(AR(p)\)模型的偏自相关函数，再利用模型偏自相关函数的截尾性估计\(p\)
利用拓展的自相关系数估计\(ARMA(p,q)\)模型的\(p,q\)

3.2 实践操作

3.2.1 例1

理论模型\(MA(1)\)： \[ Y_t = e_t-0.9e_{t-1} \]

时间序列数据：

eg1 <- arima.sim(model = list(ma=-0.9),n=200,sd=1)

下面我们开始模型识别。

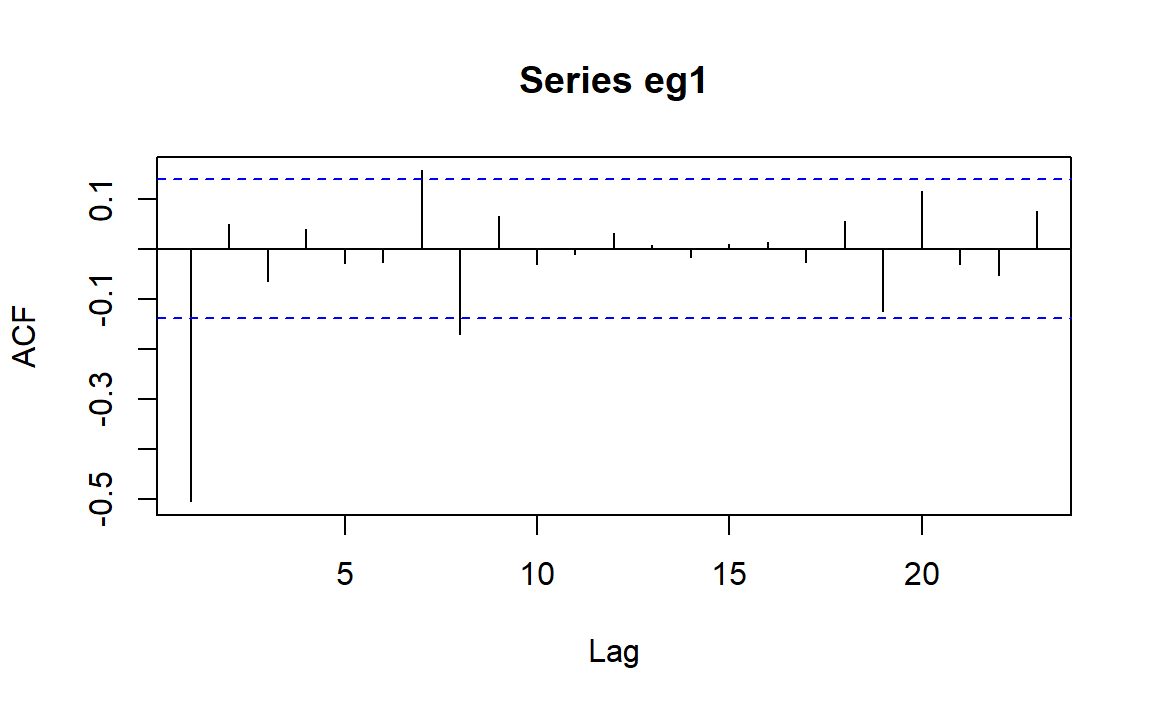
先绘制样本自相关函数图：

acf(eg1)

利用函数acf绘制样本自相关图。上下两条虚线表示，自相关系数是否显著为0的临界值。此时的临界值是基于白噪声过程中的近似大样本标准误差，即\(1/\sqrt{n}\)。

可以看到滞后1阶ACF值显著不为0，滞后7，8阶稍微超过临界值。可以考虑一下\(MA(q)\)模型。

修正一些ACF临界值：

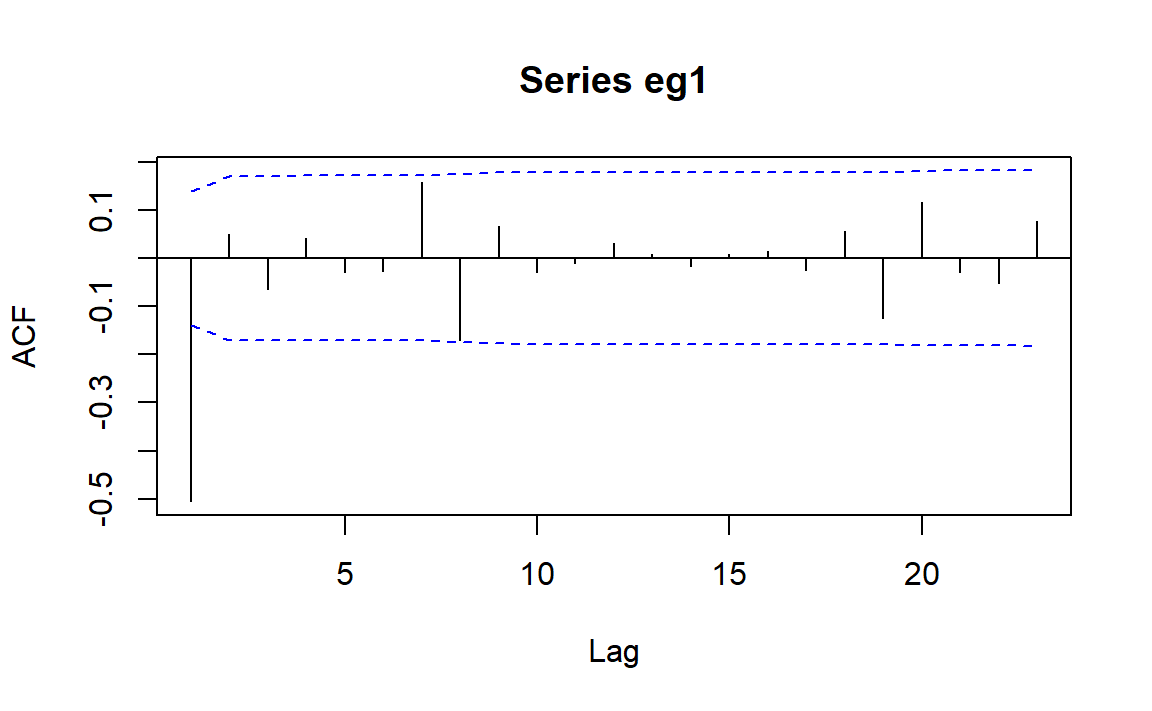
# 加入ci.type="ma"，标准临界值是根据ma模型样本自相关系数的近似正体分布绘制的
acf(eg1,ci.type="ma")

可以看到，此时只有滞后1阶ACF显著不为0，意味着我们可以考虑为这个序列拟合\(MA(1)\)模型。

3.2.2 例2

理论模型\(MA(2)\)： \[ Y_t = e_t-e_{t-1}+0.6e_{t-2} \]

时间序列数据：

eg2 <- arima.sim(model = list(ma=c(-1,0.6)),n=200,sd=1)

下面我们开始模型识别。

先绘制样本自相关函数图：

acf(eg2)

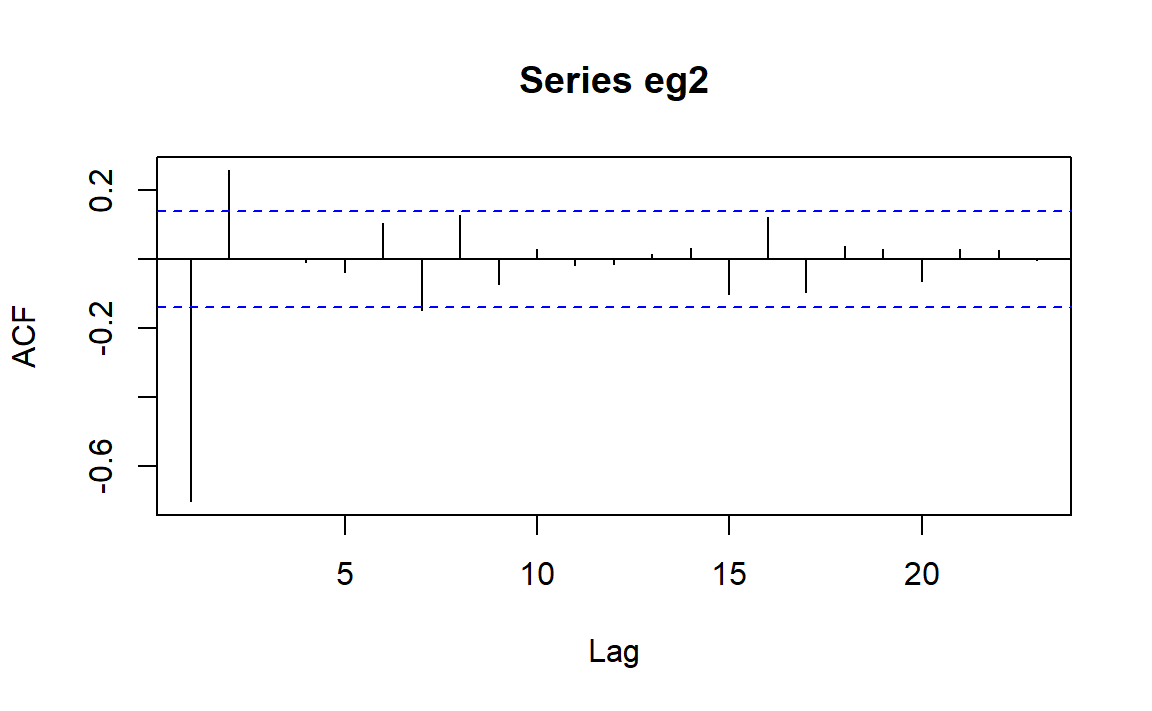
可以看到比较明显的滞后截尾性，滞后1，2阶ACF值显著不为0，滞后7阶稍微超过临界值。可以考虑一下\(MA(q)\)模型。

修正一下ACF临界值：

acf(eg2,ci.type="ma")

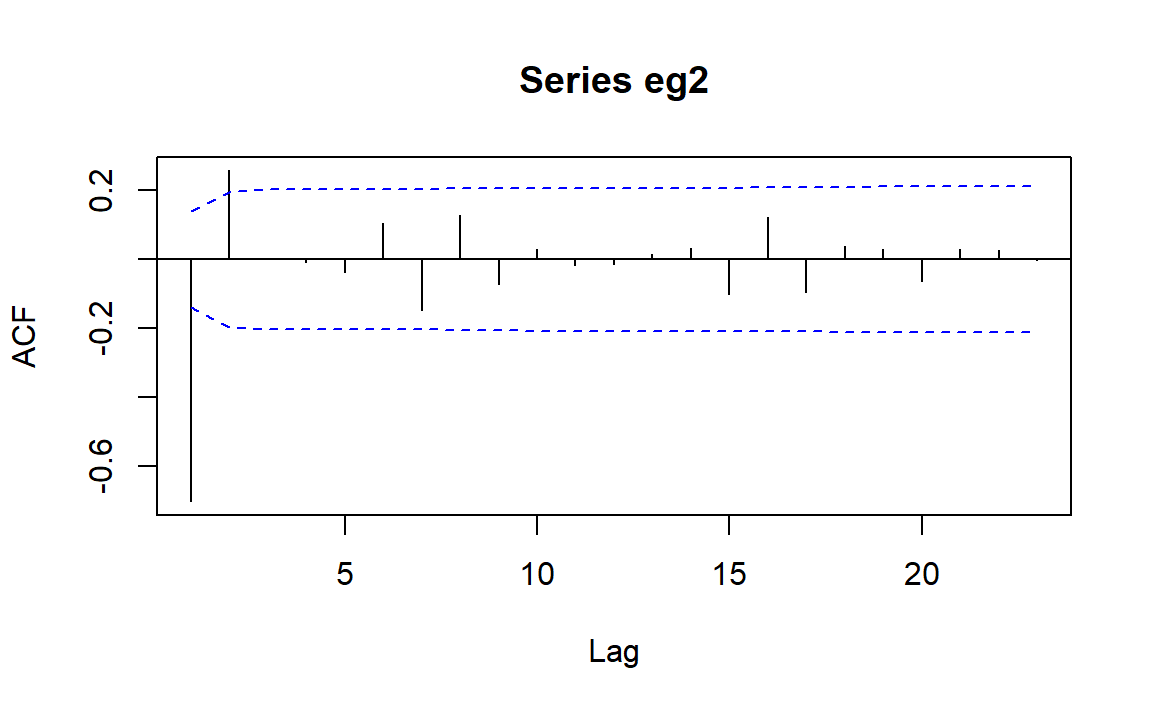
可以看到，此时只有滞后1，2阶ACF显著不为0，意味着我们可以考虑为这个序列拟合\(MA(2)\)模型。

3.2.3 例3

理论模型\(AR(1)\)： \[ Y_t = 0.9Y_{t-1}+e_t \]

时间序列数据：

eg3 <- arima.sim(model = list(ar=0.9),n=200,sd=1)

下面我们开始模型识别。

先绘制样本自相关函数图：

acf(eg3)

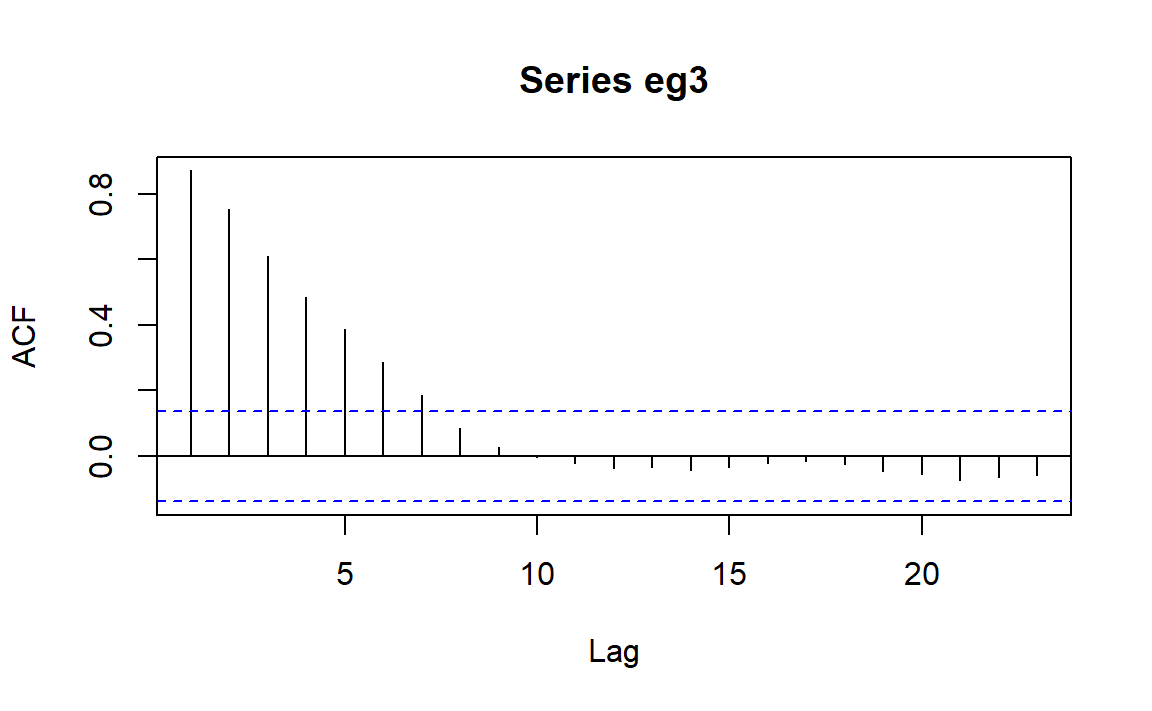
与理论图像1.5不太一致，样本ACF更像是线性递减而不是指数递减，并且不是一直保持大于0。但这并不影响我们去考虑\(AR(p)\)模型。

观测样本偏自相关系数PACF图像：

pacf(eg3)

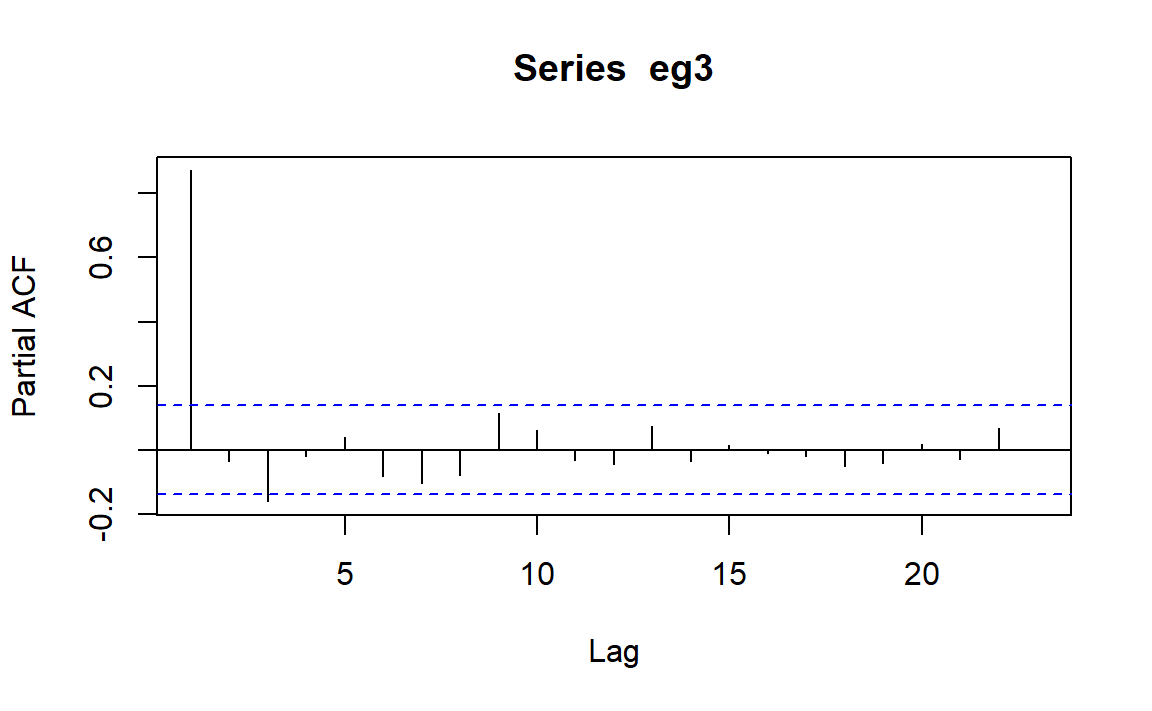
可以看到，此时滞后1阶PACF显著不为0，滞后3阶稍微超过临界值，意味着我们可以考虑为这个序列拟合\(AR(1)\)模型，但在模型诊断时需要进一步研究滞后3阶的显著性。

3.2.4 例4

理论模型\(AR(2)\)： \[ Y_t = 1.5Y_{t-1}-0.75Y_{t-2}+e_t \]

时间序列数据：

eg4 <- arima.sim(model = list(ar=c(1.5,-0.75)),n=200,sd=1)

下面我们开始模型识别。

先绘制样本自相关函数图：

acf(eg4)

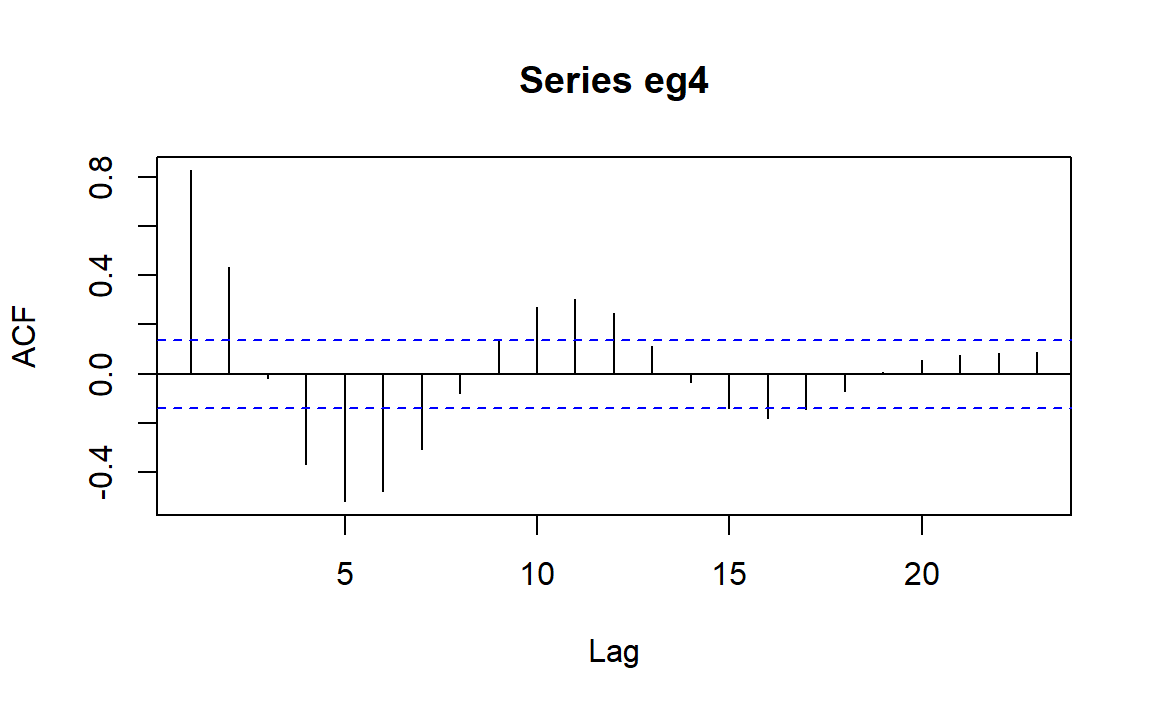
图像呈阻尼正弦波动曲线，可以考虑一下\(AR(p)\)模型。

观测样本偏自相关系数PACF图像：

pacf(eg4)

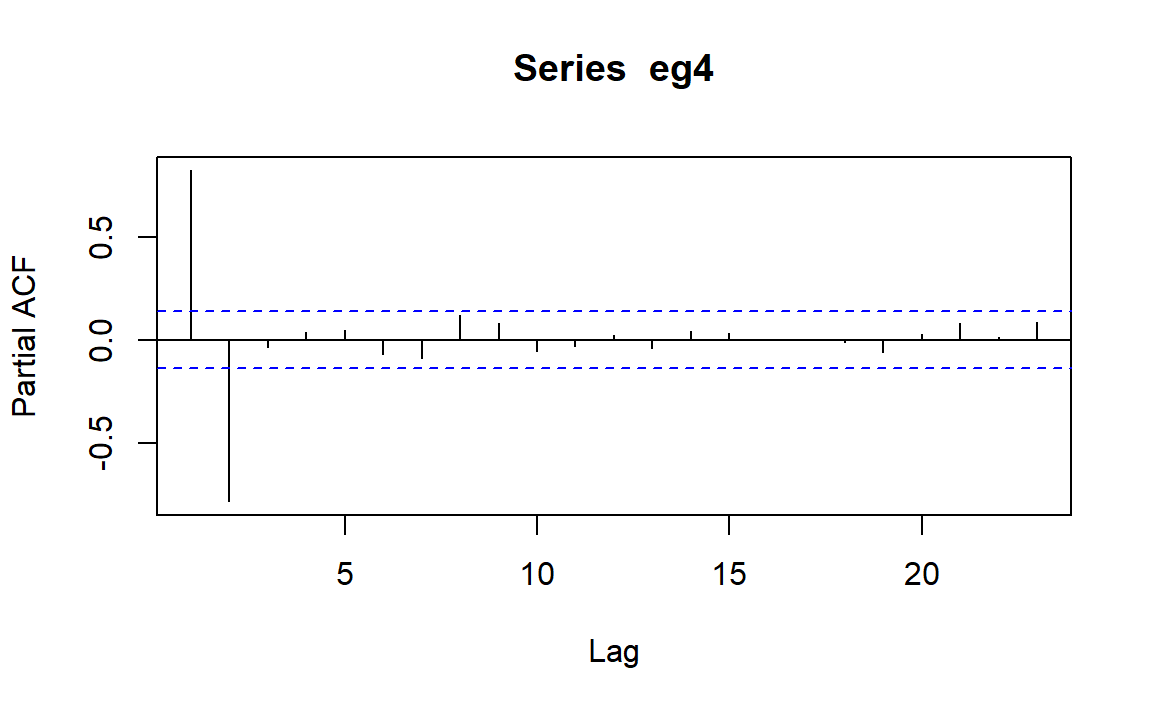
可以看到，此时只有滞后1，2阶PACF显著不为0，意味着我们可以考虑为这个序列拟合\(AR(2)\)模型。

3.2.5 例5

理论模型\(ARMA(1,1)\)： \[ Y_t = 0.6Y_{t-1}+e_t+0.3e_{t-1} \]

时间序列数据：

eg5 <- arima.sim(model = list(ar=0.6,ma=0.3),n=100,sd=1)

下面我们开始模型识别。

先绘制样本自相关函数图：

acf(eg5)

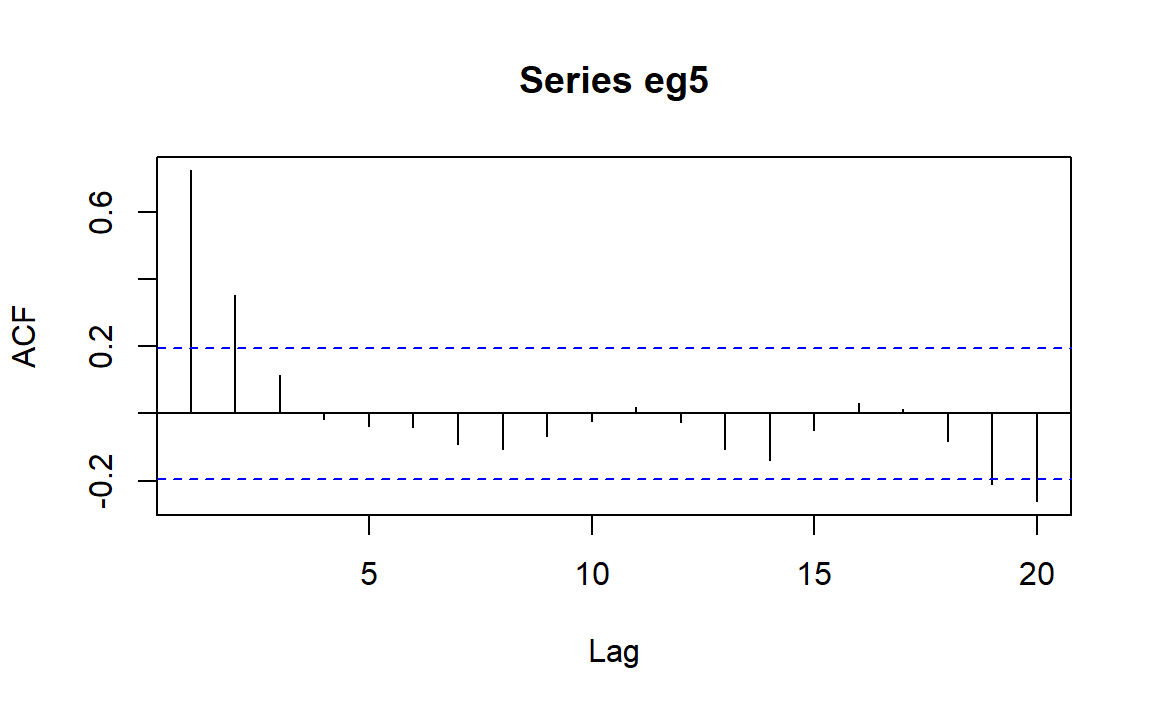
样本PACF：

pacf(eg5)

综上，看起来我们应该为序列拟合\(AR(1)\)模型。

但是，我们看一下拓展的自相关系数EACF：

eacf(eg5)
#> AR/MA
#>   0 1 2 3 4 5 6 7 8 9 10 11 12 13
#> 0 x x o o o o o o o o o  o  o  o 
#> 1 x o o o o o o o o o o  o  o  o 
#> 2 x x o o o o o o o o o  o  o  o 
#> 3 x o o o o o o o o o o  o  o  o 
#> 4 x x o x o o o o o o o  o  o  o 
#> 5 x o x x o o o o o o o  o  o  o 
#> 6 x x x o o o o o o o o  o  o  o 
#> 7 x x o o o o o o o o o  o  o  o

这表示我们应该为该序列拟合\(ARMA(1,1)\)模型。

接下来我们看一下前4个例子的EACF：

eacf(eg1)
#> AR/MA
#>   0 1 2 3 4 5 6 7 8 9 10 11 12 13
#> 0 x o o o o o x x o o o  o  o  o 
#> 1 x x o o o o o x o o o  o  o  o 
#> 2 x x o o o o o x o o o  o  o  o 
#> 3 x x o o o o o x o o o  o  o  o 
#> 4 x x x o x o o x o o o  o  o  o 
#> 5 x o o o x o o x o o o  o  o  o 
#> 6 x x x x x x o x o o o  o  o  o 
#> 7 x x o o o x o o o o o  o  o  o
eacf(eg2)
#> AR/MA
#>   0 1 2 3 4 5 6 7 8 9 10 11 12 13
#> 0 x x o o o o x o o o o  o  o  o 
#> 1 x x x o o o o o o o o  o  o  o 
#> 2 x x o o o o o o o o o  o  o  o 
#> 3 x x x x x o o o o o o  o  o  o 
#> 4 x o x x x o o o o o o  o  o  o 
#> 5 x x x x x o o o o o o  o  o  o 
#> 6 o x x o o o o o o o o  o  o  o 
#> 7 x o o o o o o o o o o  o  o  o
eacf(eg3)
#> AR/MA
#>   0 1 2 3 4 5 6 7 8 9 10 11 12 13
#> 0 x x x x x x x o o o o  o  o  o 
#> 1 o x o o o o o o o o o  o  o  o 
#> 2 x x o o o o o o o o o  o  o  o 
#> 3 o x o o o o o o o o o  o  o  o 
#> 4 x o x o o o o o o o o  o  o  o 
#> 5 x o x o o o o o o o o  o  o  o 
#> 6 x x x x o o o o o o o  o  o  o 
#> 7 x o x x o x o o o o o  o  o  o
eacf(eg4)
#> AR/MA
#>   0 1 2 3 4 5 6 7 8 9 10 11 12 13
#> 0 x x o x x x x o o x x  x  o  o 
#> 1 x x o x x x x o x x x  x  o  o 
#> 2 o o o o o x o o o o o  o  o  o 
#> 3 x o o o o x o o o o o  x  o  o 
#> 4 x x o o o o o o o o o  x  o  o 
#> 5 x x o o o o o o o o o  x  o  o 
#> 6 x x o o o o o o o o o  o  o  o 
#> 7 x x o o x o o o o o o  o  o  o

均支持我们之前的模型假设。

3.3 非平稳性模型

3.3.1 观察图像

序列的非平稳性经常表现在图像中，如；

时间序列图，例如图2.4，2.5；
样本ACF图，通常不会随着滞后的增加而迅速衰减。样本ACF的近似线性衰减通常被认为是时间序列非平稳并且需要差分的征兆。

3.3.2 ADF单位根检验

DF检验核心思想：对差分序列的检验等价于与原序列的AR特征多项式是否存在单位根。

增强的Dickey-Fuller检验，原假设为该过程非平稳，但差分一次后平稳，备择假设为该过程平稳。可以用于检验是差分平稳性以及趋势平稳性。

首先对过程差分AR定阶，然后利用ADF.test再进行ADF检验。

下面以随机游动为例，进行ADF检验。

首先差分AR定阶：

data("rwalk")
ar(diff(rwalk))
#> 
#> Call:
#> ar(x = diff(rwalk))
#> 
#> Coefficients:
#>      1       2       3       4       5       6       7       8  
#> -0.162  -0.123   0.004  -0.196  -0.160  -0.342   0.065  -0.323  
#> 
#> Order selected 8  sigma^2 estimated as  0.839

ADF检验，原假设为具有单位根，备择假设具有未知均值（截距）的平稳序列：

ADF.test(rwalk,selectlags = list(mode=c(1,2,3,4,5,6,7,8),Pmax=8),
         itsd = c(1,0,0))
#> Warning in interpolpval(code = code, stat = adfreg[, 3], N = N): p-value is
#> greater than printed p-value
#>   --------- ------ - ------ ----
#>   Augmented Dickey & Fuller test
#>   --------- ------ - ------ ----
#> 
#>   Null hypothesis: Unit root.
#>   Alternative hypothesis: Stationarity.
#> 
#> ----
#>   ADF statistic:
#> 
#>         Estimate Std. Error t value Pr(>|t|)
#> adf.reg   -0.036      0.059  -0.601      0.1
#> 
#>   Lag orders: 1 2 3 4 5 6 7 8
#>   Number of available observations: 51

开上帝视角，代入真实AR阶数0阶，继续ADF检验：

ADF.test(rwalk,selectlags = list(Pmax=0),
         itsd = c(1,0,0))
#> Warning in interpolpval(code = code, stat = adfreg[, 3], N = N): p-value is
#> greater than printed p-value
#>   --------- ------ - ------ ----
#>   Augmented Dickey & Fuller test
#>   --------- ------ - ------ ----
#> 
#>   Null hypothesis: Unit root.
#>   Alternative hypothesis: Stationarity.
#> 
#> ----
#>   ADF statistic:
#> 
#>         Estimate Std. Error t value Pr(>|t|)
#> adf.reg   -0.087       0.05   -1.74      0.1
#> 
#>   Lag orders: 0
#>   Number of available observations: 59

两次ADF检验的P值都大于0.1，表明有比较强的证据支持原假设，即有单位根（差分一次后平稳）。

由于：

plot(rwalk,type="o",cex=0.7)

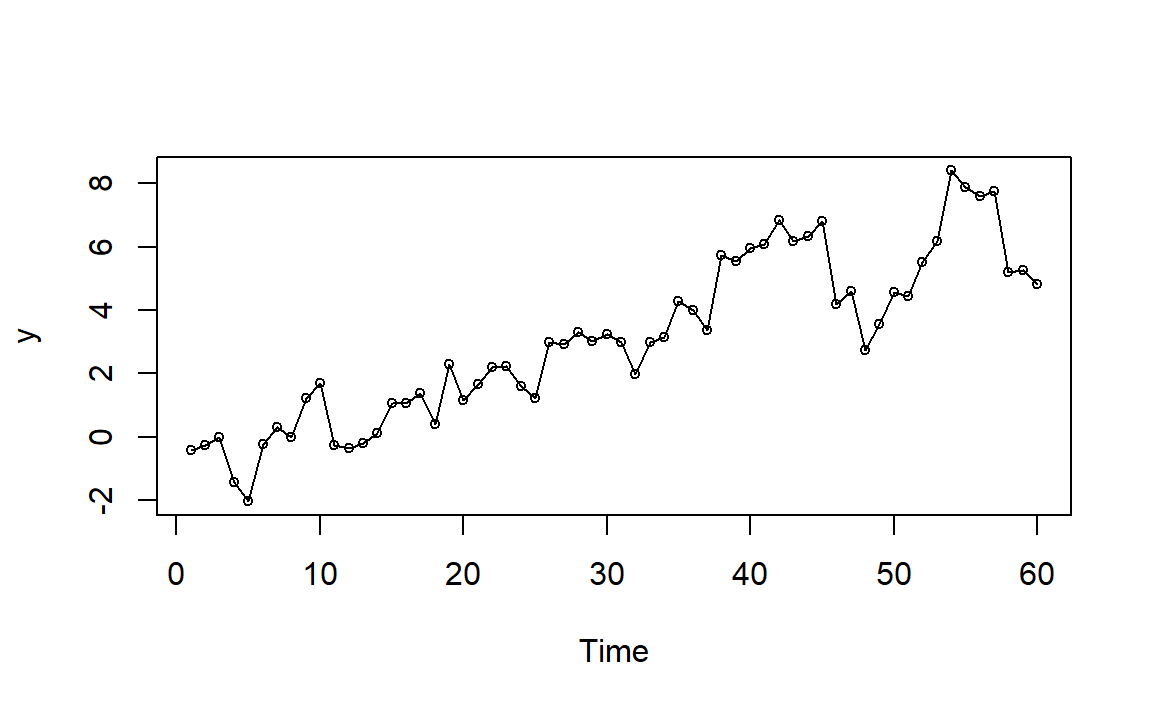
随机游动的图像看起来似乎有线性趋势，我们使用ADF检验一下：

ADF.test(rwalk,selectlags = list(mode=c(1,2,3,4,5,6,7,8),Pmax=8),
         itsd = c(1,1,0))
#> Warning in interpolpval(code = code, stat = adfreg[, 3], N = N): p-value is
#> greater than printed p-value
#>   --------- ------ - ------ ----
#>   Augmented Dickey & Fuller test
#>   --------- ------ - ------ ----
#> 
#>   Null hypothesis: Unit root.
#>   Alternative hypothesis: Stationarity.
#> 
#> ----
#>   ADF statistic:
#> 
#>         Estimate Std. Error t value Pr(>|t|)
#> adf.reg   -0.637      0.278   -2.29      0.1
#> 
#>   Lag orders: 1 2 3 4 5 6 7 8
#>   Number of available observations: 51

P值大于0.1，没有足够把握拒绝单位根假设。

ADF.test(rwalk,selectlags = list(Pmax=0),
         itsd = c(1,1,0))
#>   --------- ------ - ------ ----
#>   Augmented Dickey & Fuller test
#>   --------- ------ - ------ ----
#> 
#>   Null hypothesis: Unit root.
#>   Alternative hypothesis: Stationarity.
#> 
#> ----
#>   ADF statistic:
#> 
#>         Estimate Std. Error t value Pr(>|t|)
#> adf.reg    -0.39      0.112   -3.49     0.05
#> 
#>   Lag orders: 0
#>   Number of available observations: 59

P值约为0.05，有较弱的证据拒绝原假设，即认为该序列是具有线性趋势的非平稳序列（线性趋势+平稳误差），但实际上只是差分非平稳。这个例子表明，小样本下很难区分差分非平稳以及趋势非平稳。

3.4 其他识别方法

利用AIC、BIC等准则确定最佳子集ARMA模型。

test <- arima.sim(model = list(ar=c(rep(0,11),0.8),
                               ma=c(rep(0,11),0.7)),n=120)
res <- armasubsets(test,nar = 14,nma = 14,y.name = "test",
                   ar.method = "ols")
plot(res)

从图像推测从为ARMA(12,12)模型。