4 均匀分布随机数生成

set.seed(1024)

4.1 习题

习题1

易证。

习题2

解：

将[0,1]等分为\(k\)段，每个端点分别为\(x_i=i/k,i=0,\dots,k\)，考虑左闭右开区间，如果给定点\(x\)落在\(x_i\le x<x_{i+1}\)中，有\(i/k\le x<(i+1)/k\)，即\(i\le kx <i+1\)，\(\lfloor kx \rfloor=i\)，若\(x<0\)或\(x>1\)报错。

runif.chisq.test <- function(x, k)
{
  y <- rep(0,k)
  for (i in seq_along(x)) {
    j <- floor(k*x[[i]])  # 第j段
    if(x[[i]]==1){
      y[[k]] <- y[[k]]+1
    }else if(j<0 | j>=k){
      stop("there is value of x out of [0,1]")
    }else{
      y[[j+1]] <- y[[j+1]]+1
    }
  }
  chisq.test(y)
}

测试一下：

x <- runif(1000)
k <- 10
runif.chisq.test(x,k)
#> 
#>  Chi-squared test for given probabilities
#> 
#> data:  y
#> X-squared = 3.06, df = 9, p-value = 0.9619

通过检验。

x <- rnorm(1000)
x <- x[x>=0&x<=1]
k <- 10
runif.chisq.test(x,k)
#> 
#>  Chi-squared test for given probabilities
#> 
#> data:  y
#> X-squared = 20.047, df = 9, p-value = 0.01763

显著性水平0.05下拒绝原假设。

习题3

解：

类似地，这里对输入数据的最小值与最大值之间等分\(k\)段，每个端点分别为\(x_i=i/k,i=0,\dots,k\)，考虑左闭右开区间，如果给定点\(x\)落在\(x_i\le x<x_{i+1}\)中，有\(i/k\le x<(i+1)/k\)，即\(i\le kx <i+1\)，\(\lfloor kx \rfloor=i\)。

# F为分布函数
random.chisq.test <- function(x, k, F)
{
  library(purrr)
  
  xmin <- min(x)
  xmax <- max(x)
  d <- xmax-xmin
  j <- floor(k*(x-xmin)/d)
  y <- rep(0,k+2)
  for (i in seq_along(x)) {
    if(x[[i]]==max(x)){
      y[[k+1]] <- y[[k+1]]+1
    }else{
      y[[j[[i]]+2]] <- y[[j[[i]]+2]]+1
    }
  }
  p <- seq(xmin,xmax,length.out = k+1) %>% 
    map_dbl(F)
  p <- c(p[[1]],diff(p),1-p[[k+1]])
  chisq.test(y,p = p)
}

测试：

x <- rnorm(1000)
k <- 10
random.chisq.test(x,k,pnorm)
#> Warning in chisq.test(y, p = p): Chi-squared approximation may be incorrect
#> 
#>  Chi-squared test for given probabilities
#> 
#> data:  y
#> X-squared = 8.422, df = 11, p-value = 0.6751

x <- runif(1000)
k <- 10
random.chisq.test(x,k,pnorm)
#> 
#>  Chi-squared test for given probabilities
#> 
#> data:  y
#> X-squared = 2044.9, df = 11, p-value < 2.2e-16

通过测试。

习题4

解：

这个应该是下一节的内容，不过无所谓啦。先得到它的分布函数为 \[ F(x) = \frac12x+\frac12x^2,\quad0\le x\le1 \]

1、逆变换法：

先求\(F^{-1}\)为： \[ F^{-1}(u) = -\frac12+\sqrt{2u+\frac14} \] 从而定义函数：

rng.x1 <- function(n)
{
  -0.5+sqrt(2*runif(n)+0.25)
}

测试：

n <- 1000
x <- rng.x1(n)
hist(x,freq = FALSE)
y <- seq(0,1,0.01)
z <- 0.5+y
lines(y,z,col="red")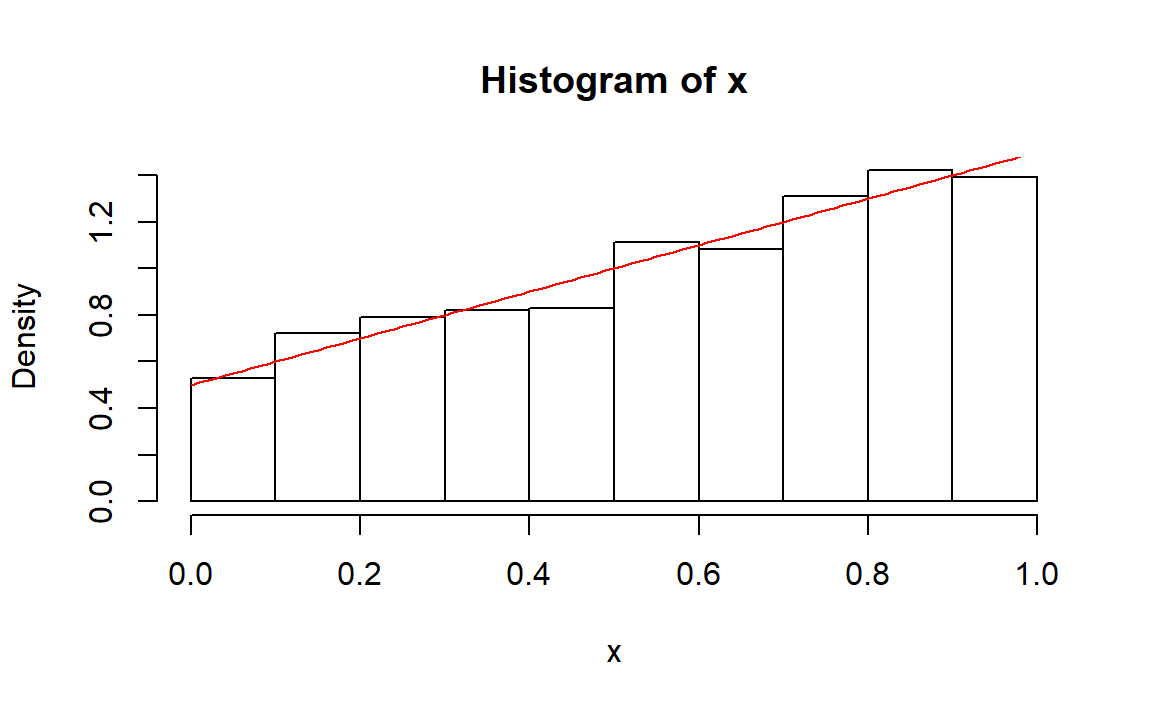

基本吻合。

2、舍选法

就是拒绝采样啦，取提议分布为均匀分布\(U[0,1]\)，则\(c=1.5\).

rng.x2 <- function(n)
{
  x <- runif(n)
  y <- runif(n,0,1.5)
  s <- x[y<=0.5+x]
  list(samples = s, eff = length(s)/n)
}

测试：

n <- 1000
x <- rng.x2(n)
hist(x$samples,freq = FALSE)
y <- seq(0,1,0.01)
z <- 0.5+y
lines(y,z,col="red")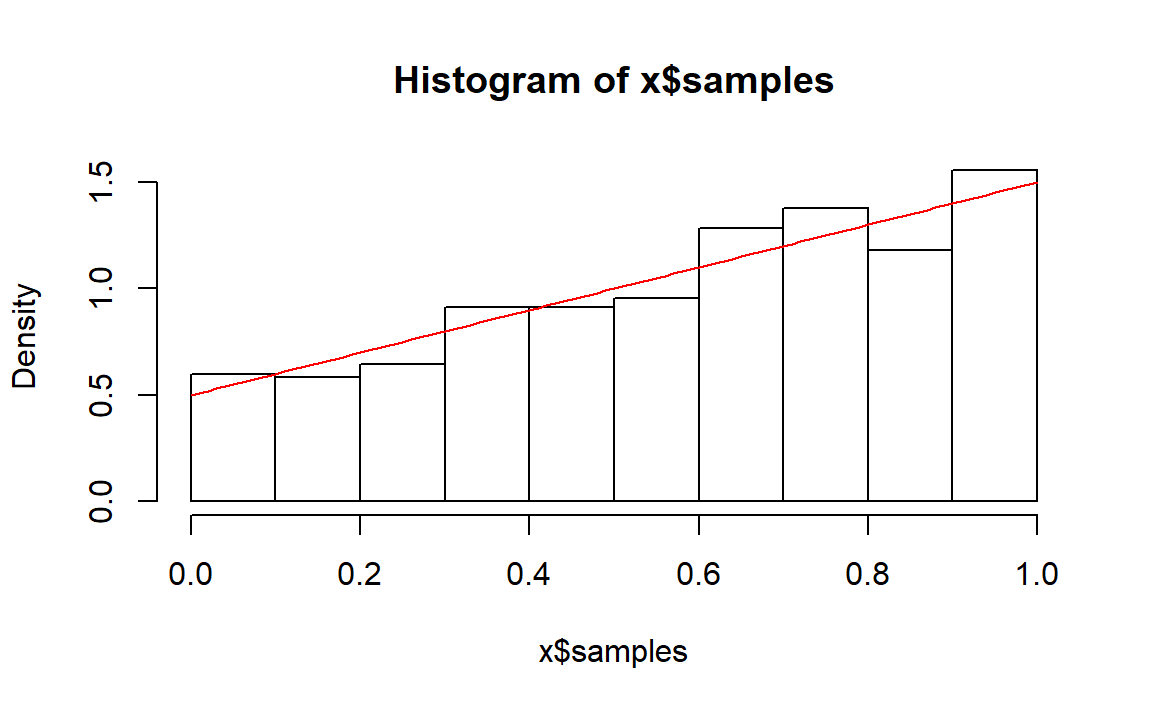

基本吻合。看一下效率：

x$eff
#> [1] 0.669

理论上的效率为\(2/3\)。

3、复合法

将梯形面积分解为一个矩形跟一个三角形，两者面积都是0.5。

rng.x3 <- function(n)
{
  i <- runif(n)
  x <- runif(n)
  # 小于等于0.5保持值，大于0.5开平方
  x[i>0.5] <- sqrt(x[i>0.5])
  x
}

测试：

n <- 1000
x <- rng.x3(n)
hist(x,freq = FALSE)
y <- seq(0,1,0.01)
z <- 0.5+y
lines(y,z,col="red")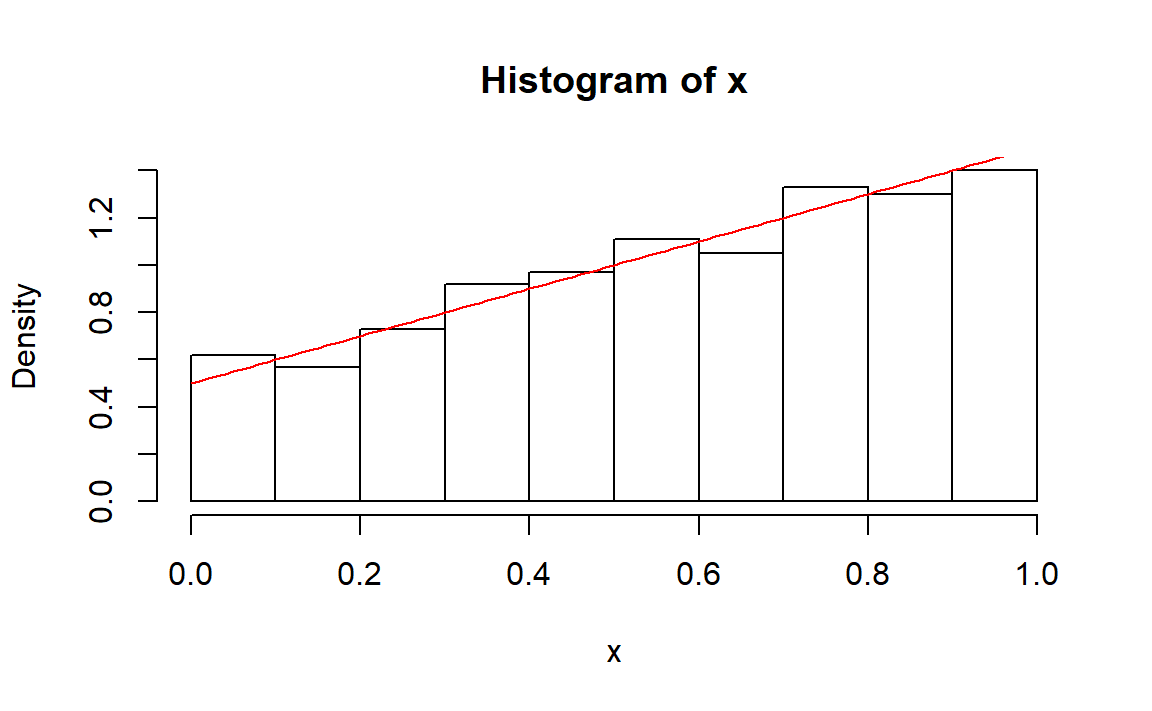

比较算法的效率？除了舍选法会拒绝点之外，其余两者算法都是全部接受点的。看一下函数的运行时间吧，虽然这个比较粗糙，因为跟算法编码的设计有关，不一定是算法本身的问题：

n <- 10000000
t1.1 <- proc.time()
x <- rng.x1(n)
t1.2 <- proc.time()
t1 <- t1.2-t1.1
t2.1 <- proc.time()
x <- rng.x2(n)
t2.2 <- proc.time()
t2 <- t2.2-t2.1
t3.1 <- proc.time()
x <- rng.x3(n)
t3.2 <- proc.time()
t3 <- t3.2-t3.1
df <- data.frame(`逆变换法`=t1[3][[1]],`舍选法`=t2[3][[1]],`复合法`=t3[3][[1]])
knitr::kable(df)

逆变换法	舍选法	复合法
0.52	1.06	1.1

总的来说，逆变换法要更好点，舍选法要稍差点。